http://www.rexresearch.com/piggott/piggott.htm
http://www.freepatentsonline.com/1006786.pdf
Author's note: The projects associated with this document had to be cancelled due to unforeseen circumstances. The document itself might still be valuable for the various insights and suggestions that are offered. The reader will have to evaluate the contents here for his own purposes.
Restricted Circulation: Currently, this document is
privately circulated and is not visible to
search engines.
Notice: This document is now obsolete and will no longer be updated.
Electromagnetic Test Cells,
Part One: Basic Technology
Copyright 2013 by Brian Fraser
last modified 2-24-14b
May be freely copied for non-commercial
and educational purposes only. Author retains
all rights to maintain document.
"Cast your bread on the
surface of the waters,
for you will find it after many days."
Ecclesiastes 11:1
Table of Contents:
The need for investigation
Piggott's experiments
Farrow's experiments
Hutchison's experiments
Nipher/Brown experiments
Discussion
Warnings
Van de Graaff generators
Spherical electrode construction
Copper sulfate resistors
Insulators
Polarity Tests
Induction coils and transformers
Types of coil windings
Replication scheme for Farrow and Piggott experiments
Rotating pulsed electrical fields
The need for investigation of special electromagnetic effects:
When one reviews the literature on electromagnetism, certain "neglected topics" show up that have never been investigated but which seem to deserve a lot more study because they have very consequential implications. This is stuff that universities ignore and is not in the science text books, not even in books on so-called "advanced electromagnetics". I like to think of normal physics as "space divided by time" but the kind of physics addressed here is just the inverse: "time divided by space". Investigating such "non-local physics" requires some weird mental gymnastics: configurations that seem to be useless and pointless from the standpoint of physics-for-public-consumption turn out to be useful and may have astonishing effects. Physicists normally write off these strange occurrences as "anomalies" and don't bother investigating them further, for to do so, would, in their view, be a "waste" of time and money. Hence, it is the intent of this paper to explore these topics in more detail, and to give simple tutorials on the readily accessible technology needed to investigate the reported effects. Some historical examples are given below.

http://www.rexresearch.com/piggott/piggott.htm
http://www.freepatentsonline.com/1006786.pdf
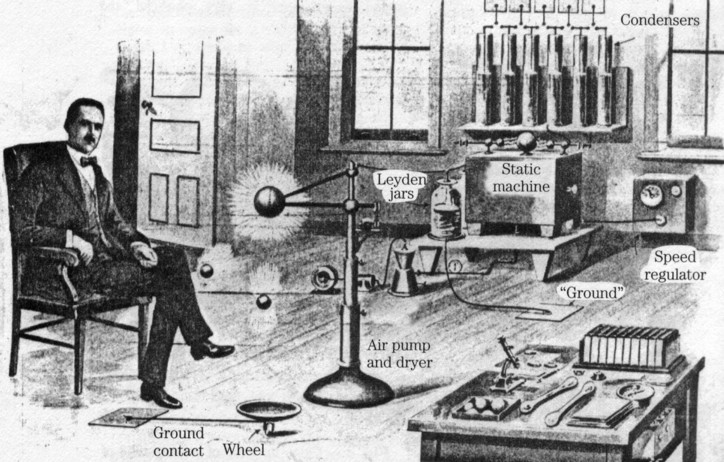
Piggott patented an electrostatic machine for use in "space telegraphy" (filed 1903, issued 1911). In the course of testing his machine, he discovered some levitation effects on silver balls. Today's textbook physics cannot account for these effects. There are more details at: http://scripturalphysics.org/4v4a/ADVPROP.html#PiggottLinks

http://www.rexresearch.com/farrow/farrow.htm Ruhmkorff coil http://www.sparkmuseum.com/INDUCT.HTM
Farrow demonstrated a weight reduction effect by means of a "condensing dynamo" circa 1911. The device was not patented and the internals of the machine are not described. Various photos give the impression of an old-style Ruhmkorff induction coil with the terminals of the secondary connected to long wires. The machine was placed on top of a book, on top of a spring scale (not a balance scale). When turned on, the combination gradually lost 3 ounces of weight. Today's textbook physics cannot account for these effects, if indeed they are real. There is more information at: http://scripturalphysics.org/4v4a/ADVPROP.html#FarrowLinks
"In 1979, Hutchison claims to have discovered a number of unusual phenomena, while trying to duplicate experiments done by Nikola Tesla. He refers to several of these phenomena jointly under the name “the Hutchison effect”, including: levitation of heavy objects; fusion of dissimilar materials such as metal and wood; while lacking any displacement, the anomalous heating of metals without burning adjacent material; the spontaneous fracturing of metals; changes in the crystalline structure and physical properties of metals; disappearance of metal samples." http://en.wikipedia.org/wiki/Northern_Mysteries
The Hutchison effect has never been replicated publicly by an independent third party. Some people regard the effect as very credible but others regard it as pure folklore. My own suspicion is that there are indeed such effects and that they are "non-local" in their nature. This kind of effect can be produced by electric and magnetic fields, which are themselves non-local. The public scientific community has little understanding of non-local effects (except as applied to quantum mechanics), and would easily dismiss them as "experimental error" or as "anomalies" or even as hoaxes. As Antoine Lavoisier (the father of modern chemistry) , told his fellow Academicians, "Stones cannot fall from the sky, because there are no stones in the sky!" In the popular scientific view, if something cannot happen, it simply does not, despite evidence to the contrary. "Galileo, there is no need for us to look through your telescope!" Hence, the Hutchison effect is easily written off and ignored by institutional science. But if it is a real and reproducible effect, the scientific insights would be enormous.
In a similar category is ORME (Orbitally Rearranged Monoatomic Elements). David Hudson is the authority on this topic and you can read his lectures at http://www.asc-alchemy.com/hudson.html See especially "David Hudson: Sakarov's theory of gravity" regarding disappearance of materials and antigravity effects. Statements in these lectures are both hard to believe and hard to ignore. But they fit the theme of non-local physics.
There are probably some examples in astronomy as well. Pulsars "disappear" from the reference system many times per second. They blink on and off and in the unusual case where they can be photographed, it is necessary to synchronize the telescope's camera shutter so that the object can be photographed (with a time exposure) in the "on" state and then the "off" state. The rapid blinking is thought to be caused by rotation, much like a lighthouse beacon. It is difficult to conceive of a mechanism whereby a star can "beam" its energy in one dimension even if it is rotating. But even so, this would involve a dimensional effect. The dimension here is simply spatial, with only one dimension active of the three. But it is more likely that the light is non-directional and is being split between spatial and temporal dimensions. Likely the star will eventually become localized completely in space like a normal star, or become localized in three-dimensional time and disappear completely from a spatial reference system. ( http://en.wikipedia.org/wiki/Pulsar )
Additionally, I believe UFOs are man-made machines that thoroughly utilize non-local physics. So it is not surprising that there are many reports about UFOs being semitransparent. ( http://unitedstatesufo.blogspot.com/2011/12/semi-transparent-long-tubular-ufo.html ; http://www.examiner.com/article/colorado-couple-v-shaped-semi-transparent-ufo-flew-low-and-silent ; http://the-v-factor-paranormal.blogspot.com/2012/02/huge-semi-transparent-v-shaped-ufo-over.html
http://ufodigest.com/article/illinois-witnesses-watch-triangle-ufo-become-transparent )And who has not heard of the Philadelphia Experiment where (it is claimed) men and materials disappear or merge with bizzare and lethal effects. ( http://en.wikipedia.org/wiki/Philadelphia_Experiment )
See also "Utilization of non-local Effects" .
See also:
http://www.hutchisoneffect.ca/
http://www.slideshare.net/johnkhutchison/hutchison-effect
http://www.youtube.com/watch?v=tnBdhsXl088&feature=related
http://www.youtube.com/watch?v=Gf_z2QFQxLk&NR=1
http://www.skywise711.com/Skeptic/Hutchison/hutchison.html
http://www.americanantigravity.com/documents/The-Ultimate-Hutchison.pdf
There are experiments that suggest an object's weight depends on local gravity, its mass, and its electrical history.
http://www.rexresearch.com/nipher/nipher1.htm#1 (studies on gravitation)
http://en.wikipedia.org/wiki/Francis_Eugene_Nipher
http://kirkwood.patch.com/listings/nipher-middle-school
http://library.wustl.edu/units/spec/archives/guides/pdf/nipher.pdf
http://genforum.genealogy.com/nipher/messages/2.html(Dr. Nipher was an esteemed educator and was professor of physics at Washington University at St. Louis, Missouri. He was also president for several years of the St. Louis Academy of Science and of the Engineers Club. He wrote several valuable papers in the late 1800s. Nipher Middle School was named after him.)
See also Biefeld-BrownEffect
The intent here is to reproduce the above reported effects and to discover the new science (not the technology) behind them.
As can be conjectured from the above illustrations, some of the sought for effects seem to depend on the production of high voltage pulses that repeat several times per second, and which have fast rise times and slower fall times, such as the pulses delivered by an automotive ignition coil. They evidently must be monopolar (+,+,+ or -,-,-) and not bipolar (+,-,+,-,+,-). This conjecture is based on the fact that pulsed electric fields produce a flow of electromagnetic momentum (see Poynting vector). Unidirectional momentum would be produced by monopolar asymmetric pulses. Unfortunately, Piggott says nothing about pulsed electric fields in his levitation experiments, just that his machine can produce such fields. However, his machine shown in the experiment does have spark gaps, implying the use of pulsed fields. There is also a small Leyden jar to (the left of the machine) which connects to the sphere near the levitating balls. This may add a DC bias to the pulsed field (another conjecture). The cabling method also implies a large "loop area" —something that electrical engineers would notice immediately—between the high tension terminal and ground. Is this relevant to the experimental effect or not?
Engineers usually try to avoid loop areas because they increase inductance and radiative effects. Where they cannot be avoided, such as in long-distance power transmission, the "directed areas" enclosed by the wires are regularly "flipped" by systematically transposing the wires. This reduces inductive effects, which are normally not wanted in ordinary electrical electrical wiring.
http://en.wikipedia.org/wiki/Transposition_(telecommunications)Telephone circuits use twisted pairs to reduce inductance and interference ("cross-talk") effects. There may be hundreds of pairs in a cable bundle, and the cable could be miles long and so reduction of cross-talk is important. Long open loops increase inductance and the tendency to radiate, but with twisted pair the loop areas are small, and adjacent loops have oppositely directed areas, which makes them less susceptible to external interference. Twisted pair may still have significant capacitance, which will cause signal degradation with distance. This effect was reduced in the old telephone circuits by placing "loading coils" at appropriate distances along the path, or by using wires that were coated with an iron based compound. Later, the use of coaxial cable obviated these problems. http://en.wikipedia.org/wiki/Loading_coil ; http://en.wikipedia.org/wiki/Mu-metal
Farrow's setup explicitly required long wires from the high tension terminals. However, he (apparently) does not use a spark gap on the high tension side. A spark discharge is rich in broad spectrum electromagnetic energy, and will cause an attached resonant system, such as an antenna, to emit Hertzian waves (see third illustration below). This was the usual use of these coils in those days. But production of levitation, not radio waves, seems to be the intention of this particular setup.
The sections below give a basic, hobbyist-oriented description of what kind of machines can produce these kinds of pulsed electric fields, along with some historical notes and occasional construction hints. The intent is to stick to basic technologies of the kind that existed around the 1920s, although some modern substitutions are used due to their availability and better reliability (why use double cotton covered wire, for instance?). The main purpose is to detect an effect, and to see if these historical reports have credibility and a basis in fact. The basic technology to produce these strange effects has been around for over a hundred years. What has not been published is the science behind them.
Far more advanced technology can be found in the links at Capacitor Tests.
Operation of the various equipment or configurations shown in this document is very dangerous. There are the usual electrical hazards of household AC. There are other hazards associated with the high voltages used (500,000 volts). Additionally, the sought for effects, the hazards of which, are not understood at this point, are presumed to be lethal or unhealthful. Historically, some scientists and engineers experimenting with similar devices have been killed by strange and unexpected effects. Some of the effects are completely unpredictable and unexpected (time, location, and type) If you experiment with these machines, you do so entirely at your own risk. If you are a young, testosterone crazed male, convinced of your own IMMORTALITY, you definitely need the supervision of a wise, cautious, discerning, sane adult —preferably one with a background in electrical engineering. If you run these experiments, you MUST have a safety partner equipped with a set of specific safety procedures to handle "what if" situations.
"Be dead certain, or you will certainly be dead"
—the electrician's warningThe descriptions here are intended as a summary of principles for the skilled experimenter. There is plenty of room for creative imagination.
There are many types of static machines that can produce static electric fields of millions of volts. Their history is very interesting and supplies valuable background for the experiments proposed here. Some informative links are as follows:
http://en.wikipedia.org/wiki/Electrostatic_generator
http://en.wikipedia.org/wiki/Electrostatic_induction
http://en.wikipedia.org/wiki/Van_de_Graaff_generator
"The Van de Graaff Generator", Paolo Brenni (1999) http://lyonel.baum.pagesperso-orange.fr/sis.html
"DC Accelerators", E.Cottereau, http://cas.web.cern.ch/cas/pruhonice/pdf/dc-accel-DB1.pdf
FN Tandem Van de Graaff Accelerator at Notre Dame, Larry Lamm (2009) http://www.jinaweb.org/outreach...June2009.pdf
http://en.wikipedia.org/wiki/Wimshurst_Machine
http://en.wikipedia.org/wiki/Triboelectric_effect
http://www.teslauniverse.com/nikola-tesla-article-possibilities-of-electro-static-generatorshttp://www.physicsplayground.com/apps/forums/show/14015282-general-discussion (this group appears to have the required equipment and expertise to investigate the effects listed above. I have expressed my interest.)
"The Van de Graaff Generator", Trump, Merrill & Safford (1938). http://lateralscience.co.uk/VDG/VDG.html This machine outputs a "half a million volts at around 200uA". (That is sort of equivalent to 100 watts because the 200uA is continuous short circuit amps. It is probably suitable for the Piggott replication experiment. Additional spark gap switches and pulse forming are needed to get the impulse power levels up to a modest 10 million watts (preferrably higher) with a repetition rate of 10 pulses per second (preferrably higher). I am trying to design one in this range that should be somewhat easier to build.)
The best known of these are the Van de Graaff generator and the Wimshurst "influence" machine. Only the Van de Graaff will be considered for our purposes. It is easy to understand and simple to construct, being largely a mechanical project instead of an electrical one. (See diagram at right) There are two basic categories based on the charging scheme. One type uses the triboelectric effect which generates charges based on contact-then-separation of materials having different triboelectric properties. You have experienced this effect yourself when walking across a carpet, or peeling tape off a roll. These machines are usually sold as educational science toys and are often seen in classrooms and science museums. They typically have outputs of 200,000 volts with a current of a microamp or so.
The other kind actively sprays a separately generated electric charge onto the belt, instead of using the charge developed by the triboelectric effect. This sprayed charge is much greater than that developed by "friction" and it was this feature that made all the other mechanical electrostatic generators obsolete for serious scientific purposes. A separate power supply, often a small neon sign transformer and a full-wave high-voltage rectifier, supplies an array of needles or a "comb" of pointed wires, with say, 10,000 volts of charge that is sprayed onto the moving belt constructed of insulating material. The moving belt "pumps" the upper terminal with ever increasing amounts of charge, until it is finally discharged by a spark. More than one belt can be used when the upper terminal is a racetrack shaped torus. (See Pelletron )
http://www.jinaweb.org/outreach/PIXE-PAN09/docs/Accelerator%20Presentation_June2009.pdf The main advantage of a Van de Graaff is that it can generate very high DC potentials of either polarity with just one simple, largely mechanical arrangement that has a minimum of things to adjust or assemble. These machines (and other electrostatic types) are still in wide use, mostly in connection with accelerators, ion implanters and Accelerator Mass Spectrometry:
The electrostatic accelerator . . . is one of the most versatile tools when one is using ion beams of comparatively low (i.e. a few MeV) energies. The high quality of the beam, as concerns its energy stability and emittance, the possibility of accelerating virtually every kind of ion and also continuously varying the energy over a wide range, combine to permit detailed investigations in many interesting fields of research. Among these we can mention nuclear and atomic spectroscopy, heavy-ion reactions, accelerator mass spectrometry, and ion beam analysis and modification. However, many other fields, including applied research, benefit from the use of an electrostatic accelerator.
. . .
Accelerator mass spectrometry (AMS) is an ultrasensitive technique which has found its main application in the quantification of very rare long-live radionuclides. . . . The most well-known example is 14C (10-10 % of the carbon in living organisms is 14C).Unlike a detector for the measurement of radioactivity, a mass spectrometer does not have to wait for the nuclide to decay. Thus, in the case of 14C, AMS is about 1000 times more sensitive that any radiometric method (out of 109 14C atoms, only about 10 will decay during one hour). AMS has the outstanding ability to quantify 14C-labeled substances down to levels of 10-18 moles, which is of the order of only one million molecules. The fact that AMS counts atoms and not decays results in some powerful advantages over radiometric techniques, such as highly reduced sample sizes and shortened measuring times. ( Electrostatic Accelerators Fundamentals and Applications, Ragnar Hellborg (2005), preface and p. 33)
Van de Graaff generators do have some disadvantages. They are bulky, and the moving parts (especially the belt) make them a bit hard to maintain and troubleshoot. They leak charge into the air when the humidity is high (but there are work-arounds for this problem). "Pickup" of charge by nearby objects is frequent and problematic, as it is with any monopolar type of high-voltage device (may require shielding in a Faraday cage). For an electrical machine, they are not particularly efficient—about 20%, which is low compared to 85-98% for transformers (not an important consideration here). Still, they are a good source of high voltage DC potential, and may be configured for either + or - polarity. Currents are low but adequate. A generator output of 500,000 volts @ 10 microamps equates to about 5 watts or 5 joules per second. When delivered as a single spark lasting 100 nanoseconds, that 5 joules becomes a power pulse of 50 million watts. Or if the same energy is delivered as monopolar pulses, say 25 times per second, to a test apparatus or object; each pulse would then have somewhat less than 2 million watts but still have fast rise times.
There are various links on the internet showing how to construct and run a van de Graaff:
http://mark.rehorst.com/Van_de_Graaff/ (construction experiences)
http://amasci.com/emotor/vdgbug.html (Van de Graaff Generator Debugging )
http://www.unitednuclear.com/index.php?main_page=index&cPath=90
http://home.earthlink.net/~jimlux/hv/statcalc.htm (Practical electrostatic calculations)An improved performance van de Graaff uses a high voltage source of DC (about 10 kV) to spray a charge ("brush discharge") onto the belt.
Probably the easiest way to implement this is simply to buy a high voltage DC supply that has selectable (+ or -) polarity output. It should source 10 kV at a couple of milliamps and be short circuit protected. Using a standard commercial power supply supports replication in these experiments; and you will probably spend as much or more building (and troubleshooting) one from scratch. Some possible vendors:
http://www.amazing1.com/hv-dc-power-supplies.htm
http://www.cehco.com/?page_id=98 (example of diode stacks)
http://www.hvpsi.com/pdf/D4300User-LCr04.pdf
http://www.edal.com/high-voltage-devices.php
http://www.mouser.com/The simpler commercial power supplies use a cascade voltage multiplier, the basics of which are shown in this circuit:
These could be built by a hobbyist too. See:
In our application the AC source would be a high voltage transformer (neon transformers, oil burner igniters, etc). In practice these are hard to find nowadays. Modern neon transformers have ground fault interrupters (GFI) built into them which also makes them generally unsuitable for these purposes. Microwave oven transformers cannot be used either; they are way overpowered for this application, and are not inherently current limited. If something goes wrong, you will quickly learn what V2/R means and never do it again if you survive (I speak from experience). A real transformer (NOT an autotransformer) must be used to isolate the experiment from the AC powerline. I personally do NOT recommend building such a voltage multiplier; there are too many safety problems and other variables that are a nuisance at the very least.
See below for an alternative that uses a Pulse Width Modulator and an automotive ignition coil to produce monopolar pulses suitable for charging a van de Graaff belt and for use in other experiments. However, isolation and shielding techniques are required to protect low voltage semiconductors against stray 500,000 volt static electricity.
Spherical Electrode Construction
Spherical electrodes, such as those used on van de Graaff generators are commercially available from various firms:
http://www.bestnest.com/bestnest/dept.asp?deptID=507
http://www.cn-sphere.com/stainless-steel-sphereball.html
http://engineeronline.ws/vdgspheres.htm
http://www.stainless-steel-sphere.com/304-316L-stainless-steel-sphere-balls-for-garden-s-357-371.html
http://www.rossengineeringcorp.com/toroids_spheres_corona_nuts.htmYou can also fabricate your own from serving bowls as shown below.
 |
 |
Gluing fixture for the 11 inch bowl. Note the alignment
tab in |
Stack of 5" and 11" assembled spheres sitting on top of inverted 14" serving bowl. |
Ikea sells hemispherical serving bowls (14", 11", 8", and 5") that can be assembled in to spheres (above). Here, curved strips of 0.032" aluminum are epoxied to the inside of the 11" bowl. One strip, glued to the bowl, serves as a shim-to-rim, and another epoxied on top of it and extending over the rim, serves as an alignment and attaching tab. The wooden clamping blocks are shaped to the curve of the bowl and, for assembly convenience, are temporarily glued to the hardware clamp. The aluminum strips are prepositioned and held in place with tape before being coated with epoxy and clamped.
Any required holes for belts, supports, etc. should be made before the hemispheres are assembled (permanently or temporarily). Simple holes can be drilled. Or they can be cut out with a Dremmel tool. More complex openings can be etched by a technique that involves masking, scratching, and then etching with a salt-water soaked Q-tip connected to the negative terminal of a battery or battery charger (the positive terminal connects directly to the bulk metal. See http://forums.dfoggknives.com/index.php?showtopic=17602 .
The 14 inch bowl is large enough to accommodate a double roller van de Graaff with two belt loops and two pairs of six inch long , two inch diameter rollers. The output would nominally be12 times that of a typical educational toy van de Graaff. Even more output should be obtainable with sprayed charging of the belts. (Note: these are dangerous machines!) A spherical top electrode is not an ideal shape electrically, but these shapes are readily available commercially..
Gluing setup for the 5" and the 14" bowls. This scheme does not use a shim tab. Compensation for the rim thickness is done by punching indents into the aluminum tab, and then flattening them to uniformity and correct depth in a vise. The tab is then bent to the correct curvature, held in place with tape, and then glued with 5 minute epoxy (left) or Silicone I sealant (right) and clamped. The additional drilled holes in the strip in the right photo facilitate curing of the Silicone sealant. The silicone had good adhesion and needed no mixing, but required a few days to fully cure. The corresponding hemispheres are glued on later. Not shown, a length of bare copper wire is securely taped to the inside top and bottom hemispheres before assembly. This ensures that both hemispheres will be at the same electrical potential. Also, the top hemisphere is marked "top" on the outside in case disassembly is later required, and/or a different glue is used to affix the top.
See ProjectWhitefire.html for construction details on the van de Graaff.
Resistors have several uses in megavolt machines. One use is a simple load resistor for the output. This helps to prevent ringing and overvoltage in capacitors and windings when a spark gap fires. Another use is to "crowbar" the output after the main pulse event, again to prevent ringing and polarity reversals, which are hard on capacitors (a suitable delay can be provided by a saturable magnetic switch, such as a long string of ferrite beads on a wire). Other uses include the usual voltage dividing, adjustment of RC time constants, and impedance matching (to a limited extent). Resistors must be sized for voltage standoff and power dissipation. They should also be stable over time and temperature changes (or at least predictable).
Copper sulfate resistors are commonly used in megavolt high voltage machines. They are usually constructed from transparent flexible PCV tubing, which is better than the rigid kind at absorbing the hydrostatic shock caused by a pulse. The electrodes can be end caps soldered onto a short copper tube. The "area" called for in resistivity/resistance formulas is based on a cross-section of a copper disk (do not use a bolt (screw) because the solution will leak around the threads).
http://www.pulsedpower.net/Applets/PulsedPower/CopperSulfateResistor/Copper
SulfateResistor.html Raymond J. Allen (2003)J.C.Martin on Pulsed Power, p. 129; 413-415
Resistance calculations can be done with Applets such as "Copper Sulfate Resistors", Raymond J. Allen, http://www.pulsedpower.net/Applets/PulsedPower/CopperSulfateResistor/CopperSulfateResistor.html The Applet above shows approximate values for a 300 ohm resistor that is 30 cm in length and 24 mm in diameter (active volume). It requires a concentration equivalent to 114 grams of CuSO4 5H2O (copper sulfate pentahydrate) in 1 liter of distilled water. (Concentrations of 333 grams/liter may have a tendency to crystallize when the room temperature is somewhat low.)
You can also use a Dilution Graph, such as the one pictured above at right. It uses as a standard solution 333 g copper sulfate in 1 liter of distilled water. The curves show the amount of deionized water to add to a unit volume of the standard solution to get the resistivity in ohm-cm; The formula is r = R (A/l) where rho (r) is resistivity in ohm-cm, R is resistance in ohms, A is cross-sectional area, and l is length, all in consistent units. For the above example, r = (300)p (1.2)2/30 or r= 45. That is about where the first square is on the bottom curve. And so this example would require about 20 ml of water to be added to 1 ml of standard solution to get the 300 ohms. (All that assumes I am reading the graph correctly; the text does not give an example).
The resistance can also be read with a volt-ohmmeter, but there are some caveats. Insulating films at the electrodes, electrolytic action at the electrodes, and concentration gradients, which have a battery-like effect, complicate interpretation of the readings. Often there is a capacitive effect in the reading which must be allowed to settle out (use the lowest useable scale, usually 1x; or short out the resistor for a few tens of seconds before the measurement ) Older cells may have to be "conditioned" with a few milliamps from a 9V battery for a few seconds to produce new electrode surfaces. Quick checks with a meter are nice to have, so standardize your measurement procedure so you can meaningfully interpret any changes in measurements recorded over time.
If the resistor heats up significantly during use, it has inadequate size for the required power dissipation. Run new calculations and make a bigger one.
Copper sulfate pentahydrate can be obtained from a chemical supply house, or over the internet, or from a local hardware store (it is used to kill tree roots in sewer pipes; Roebic K-77, for instance, is a usable brand, but is only 99% pure; you will have to dissolve it in distilled water, filter out the junk, and then recrystallize, filter, rinse and dry it by using the usual chemical procedures you learned in highschool).
Here is an example of a hobbyist high voltage resistor:
Actual resistor is much longer than shown here.
Shown at top is vinyl tubing ¾”OD x ½ ID, straightened by annealing at 225 F and then cooling on a 7/16" wooden dowel. The bottom electrode is made from 3 inches of soft copper tubing ½” OD Type R, soldered to two 3/8" end caps, with #12 AWG solid wire for a connection. The outside end cap has a small vent hole (next to the wire) to relieve pressure during soldering with a torch. The top electrode (not shown) has a vent hole (later plugged) and wire at its top; on its bottom there is a another additional hole centered in the cap that has a concave profile to allow bubbles and water to rise into the top electrode.
This picture shows the electrode after being pushed into the vinyl tubing. (Note the magnification effect of the clear vinyl.) The copper end caps form a tight fit with the vinyl tubing. Pressing is facilitated by heating the vinyl tubing to 200 F, and coating a couple inches of the inside with very thin layer of dishwashing detergent. The electrode is placed against something immovable (like the nearly closed jaws of a vise) and the vinyl tubing is pushed over it (which causes the warm vinyl to expand slightly).
My actual "as built" resistor has an internal active length of 17.12 inches and a calculated volume of 55.1 ml. An additional 6 ml is allowed for the inactive portion of the top electrode. The applet gave a concentration of 2.16 grams/liter for a 30k ohm resistor (active volume only). That works out to about 0.13 grams copper sulfate pentahydrate (about 1/32 of a teaspoon) in 61 ml of distilled water (too dilute to see any blue coloring; the vinyl has a slight blue tint itself).
The resistor was filled by use of a dental irrigation syringe inserted through the hole in the top electrode. A short repetitive pull/push technique is used on the syringe plunger for air pressure balance while filling the tube a little bit at a time. The resistor was then turned upside down. I held the hole closed with my finger and then squeezed the tube to get the air bubbles to rise to the top; this gave me an estimate of the amount of water I still needed to add, while leaving a small air space at the top (not visible inside the top electrode). I then re-inverted the resistor back to its normal position and worked out remaining air bubbles from the active volume.
Initial measurements with a Fluke 115 multimeter gave the following terminal-to-terminal measurements in the normal vertical position:
hr:min from fill Volts (self-generated) Ohms 00:25 0.024 56k, 61k 01:20 0.024 55k, 63k 02:30 0.012 55k, 63k 04:00 0.003 55k, 63k 06:08 0.013 57k, unstable 24:00 0.011 59k, 62k The resistance was somewhat higher than intended due to inaccuracies in weighing the tiny amount of copper sulfate. But this is definitely close enough for a first run characterization. The two values of resistance come from reversing the leads on the multimeter.
Resistors of this type will need eventual maintenance. In very dry air, the water will eventually diffuse out through the vinyl, necessitating draining, rinsing, and refilling. There may also be bacterial growth problems that have to be addressed, especially with very dilute solutions of copper sulfate.
Resistors that are used in industrial electrostatic accelerators for voltage gradient control are usually solid state metal oxide on ceramic core construction, often with integrated protective spark gaps. Their ratings are usually in the range of humdreds of megohms to several gigohms and handle voltages of ten of kilovolts.
See also:
http://en.wikipedia.org/wiki/Resistor
"Application Notes for Aqueous Electrolyte Resistors", R.E. Beverly III and Associates (2008) http://www.reb3.com/pdf/r_appl.pdfhttp://www.pulsedpower.net/Applets/PulsedPower/CopperSulfateResistor/CopperSulfateResistor.html
http://en.wikipedia.org/wiki/Electrical_resistivity_and_conductivity
http://www.reb3.com/pdf/r_appl.pdf )Links for Commercial High Voltage resistors
http://mf-powerresistor.com/High_Voltage_Resistor.htm?gclid=CPqBhJr0rroCFYs9QgodKEcAYQ
http://www.welwyn-tt.com/products/resistors/classification-search.asp?application=High_Value&technology=%25&package=%25
http://www.ebgusa.com/PDF%20Files/NEWPDF/EBGCAT09.pdf
<this section has not been written>
The Testing of a Coil for Polarity.
This is often necessary, and may be done in a variety of ways. When the coil is working, and sparks be passed between fine wires mounted on the discharger, the positive wire tip will be cold, whereas the negative end will be quite hot. In vacuo, the positive shows a purple red when the negative glows with a bluish violet. The decomposition of water, which consists of oxygen and hydrogen in the formula H2O, is readily accomplished by the secondary current, and the greatest volume of gas (hydrogen) will be evolved at the negative pole. For ready reference a summary of these facts is given below:
Positive Negative Cold wire Hot wire Anode Cathode + sign - sign Purple red Bluish violet Zinc plate (??) Carbon plate (??) (Carbon) pole Zinc pole Oxygen gas Hydrogen gas Induction Coils, How to Make, Use, and Repair Them Including Ruhmkorff, Tesla, and Medical Coils, Roentgen Radiography, Wireless Telgraphy, and Practical Information on Primary and Secondary Battery, H.S. Norrie (2nd edition, 1901) pages 44-45 http://archive.org/download/inductioncoilsho00schn/inductioncoilsho00schn.pdf
Some experimenters use a small NE-2 neon bulb (or CFL tube ?) as a polarity tester for electrostatic generators. During the test, the leads are spread apart and one lead is held between thumb and finger, and the other lead points to the electrostatic source. As the source is approached, the electrode that glows is the negative one, and the one that does not, is positive (and hopefully is pointing to the high voltage positive terminal). Caution: this test is used only at a distance from the terminal (a few feet away). Do NOT let the free lead touch or become too close to the terminal lest you get a very nasty (and possibly even lethal) shock. Do not connect any neon bulb directly into a powered circuit; the glass bulb will explode if there is no current limiting resistor. Use this technique only near static generators that produce only microamps of current.
Induction coils and transformers
Induction coils and transformers are two additional sources of high voltage. They are more difficult to construct and involve more electrical principles and concepts than a van de Graaff, but are still reasonably simple. They are more compact and can operate at higher power levels, but the voltages are usually lower. The discussion below first gives an overview of induction coils and then continues with a discussion of monopolar high voltage pulsed outputs with the emphasis on common devices like ignition coils. Then I digress a bit for a discussion about various types of coiling configurations.
http://www.sparkmuseum.com/INDUCT.HTM 1887 experimental setup of Hertz's [radio] apparatus http://en.wikipedia.org/wiki/Heinrich_Hertz
We will start off with a description of induction coils from Wikipedia:
"An induction coil consists of two coils of insulated copper wire wound around a common iron core. One coil, called the primary winding, is made from relatively few (tens or hundreds) turns of coarse wire. The other coil, the secondary winding, typically consists of many (thousands) turns of fine wire. An electric current is passed through the primary, creating a magnetic field. Because of the common core, most of the primary's magnetic field couples with the secondary winding. The primary behaves as an inductor, storing energy in the associated magnetic field. When the primary current is suddenly interrupted, the magnetic field rapidly collapses. This causes a high voltage pulse to be developed across the secondary terminals through electromagnetic induction. Because of the large number of turns in the secondary coil, the secondary voltage pulse is typically many thousands of volts. This voltage is often sufficient to cause an electric spark, to jump across an air gap separating the secondary's output terminals. For this reason, induction coils were called spark coils." http://en.wikipedia.org/wiki/Induction_coils#How_it_works
Above, are photos of induction coils that you are likely to see in a museum. They are battery powered and have primary and secondary windings like a transformer. In the old versions, both ends of each windings are brought out to brass binding posts (they were often used for wireless radio work circa 1900). The turns ratio is usually around 1:100, primary to secondary, which means that when 10 volts of AC is input on the primary, 1000 volts comes out on the secondary. This is an actually a modest voltage increase. Hence, induction coils, or "spark coils" as they are also called, are operated on pulsed DC instead of continuous AC. They operate as a "coupled inductor" instead of a transformer. The power is supplied by a battery, and the pulsations are created by a vibrating armature like those found in old-fashioned buzzers, door bells, and car horns. In the middle diagram, power from battery B is applied by closing switch K (a telegraph key, which clearly hints what this device was used for), the core becomes magnetized and attracts the armature V, causing the adjustable contacts at C to break apart. Springs and weights (not shown) can be added to the armature to control the frequency of vibration, which may be say, 5 to 1000 cycles per second. When the contacts break, the magnetic field collapses very suddenly, unlike the situation with continuous sinusoidal AC, and consequently a very high voltage is induced in the secondary, typically tens of thousands of volts. After that, the springy armature causes the contacts to close again and the cycle repeats. A capacitor across the contacts helps the primary current collapse more quickly, and also protects the contacts from erosion due to arcing.
In the old days, these spark coils were used to generate Hertzian (radio) waves for wireless telegraphy. They were connected to a spark gap, which was in turn connected to an antenna system consisting of wires, coils, and plates (the plates added capacitance). A spark discharge is rich in broad spectrum electromagnetic energy, and the pulse would cause the antenna system to electrically "ring" or "resonate" at its characteristic frequency, typically tens to hundreds of kilohertz, thereby broadcasting a pulse of crude radio waves. Today this would mess up TV and radio reception and incite riots by angry neighbors during football games, as well as unwanted visits from the FCC. In the experiments described below, provisions are made to prevent or reduce Radio Frequency Interference (RFI).
An ignition coil (below) is a specialized version of these old spark coils. They operate on the very same principles. The vibrating reed is replaced by a cam-operated switch ("breaker points") inside the distributor, and the spark produced is sent to the proper spark plug via the rotating contact in the distributor with its associated high tension wires. One end of the secondary is internally grounded to the case, or to the negative terminal of the primary.
modern ignition coil, cutaway view http://www.ignitioninfo.com/coils.html automotive 4-cylinder ignition system, mechanically timed with cam operated "breaker points" http://en.wikipedia.org/wiki/Ignition_system However, there are two noteworthy differences between ignition coils and Ruhmkorff coils. First, ignition coils only need to throw a spark about a half-inch long, but Ruhmkorff coils had no such limitation. They could throw sparks that were tens of inches long. And second, in a Ruhmkorff coil the secondary is not connected to the primary but an ignition coil "grounds" one end of the secondary to the primary.
http://twfpowerelectronics.com/~kurt/InductionCoils/12cmSpark1703.jpg
(note the "pancake" windings of the secondary (the primary is inside the white tube and is probably removable);
note that ends of the magnetic core extend beyond the coil; note that open, rather than closed, magnetic cores
(as in transformers) are used in spark coils; these give faster magnetic field collapse and higher voltages than
closed magnetic circuits; note that the secondary diameter is only about twice the diameter of the primary)
http://www.electrotherapymuseum.com/2005/Norrie/index.htm (4th edition, 1907 ?)
http://archive.org/download/inductioncoilsho00schn/inductioncoilsho00schn.pdf (2nd edition, 1901)
(note spark length of 45 inches. This is a large coil. )If you want to understand the technology of those days, or construct your own coil, the following reference is highly recommended:
Induction Coils, How to Make, Use, and Repair Them Including Ruhmkorff, Tesla, and Medical Coils, Roentgen Radiography, Wireless Telgraphy, and Practical Information on Primary and Secondary Battery, H.S. Norrie
http://archive.org/download/inductioncoilsho00schn/inductioncoilsho00schn.pdf (2nd edition, 1901)
http://www.electrotherapymuseum.com/2005/Norrie/index.htm (4th edition, 1907 ?)
It is very important to understand why the voltages produced are so high, and why the output pulse is predominantly of one polarity. The portion of voltage across an inductor due to a change in current is proportional to the inductance of the coil-and-core combination multiplied by the time rate of change of the current in the coil, mathematically expressed as: V = L(di/dt), where V is voltage, L is the inductance, and i is current. The "d /dt" symbol means "rate of change of with respect to time". The diagram below plots the current change in the primary (i1, blue) with the voltage change in the secondary (V2, red) When the switch is closed, current gradually starts building up in the primary circuit. It cannot change instantly because the inductance imposes a kind of "flywheel effect". At about the time the coil "saturates" with all the magnetic flywheel-like energy the coil can handle (the "dwell time"), the switch is designed to open (well, at least with electronic ignition systems). The field tries to collapse instantly, and if it could, the primary coil alone (without the secondary) would produce a several hundred volt spike (say 400 volts) across the switch contacts. This would erode the switch contacts and would send a high voltage spike into the car's electrical system, which could destroy sensitive equipment like radios. To prevent this, a capacitor (typically 0.3 microfarad, 1kV) is placed across the contacts. The spike then goes into the capacitor, which quickly captures the energy, allowing the field to collapse quickly. This in turn means that the di/dt term becomes enormous, and a huge voltage spike is induced in the many turns of the secondary, typically producing a pulse of 30 to 40 kilovolts (open circuit).
As the current is slowly going positive in the primary (first part of the blue curve), the current and voltage in the secondary is slowly going negative (first part of the red curve). When the contacts open, the current in the primary suddenly falls in the negative-going direction (second half). The sudden change in current (di/dt), induces a kind of "flyback voltage" ("back emf") in both coils; but the one in the primary is "caught" by the capacitor (and is not shown on the diagram); the back emf in the secondary is greatly multiplied by the 1:100 turns ratio and produces the high voltage spike in the positive direction (V2). Hence, the output is mostly monopolar, especially the fast rising edge, which is the part we are really interested in. (pretty clever, isn't it!)
http://en.wikipedia.org/wiki/Induction_coils
“So the output waveform of an induction coil is a series
of alternating positive and negative pulses, but with
one polarity much larger than the other”
Here are some typical characteristics of a High Energy Ignition coil:
Example of coil winding specs,
From a common High Energy Ignition (HEI) CoilPrimary turns: 135
Secondary turns: 11000
Turns ratio: 1 to 81.48Primary resistance 0.4 ?
Primary inductance 3.5 mH
Secondary resistance 7.8 K?
Secondary inductance 23.7 HPrimary: 12 volts at 7 amps (top of rampup)
Secondary: 80ma at 35 kV (pulse)Spark at plug: 2kV for 0.5 to 1.4 milliseconds (for 2 or 7 amps on primary)
Primary energy: E = 1/2Li2 = (0.5) (.0035)(7)2 = .086 joules
Secondary energy: E = 1/2Li2 = (0.5)(23.7)(0.080)2 = 0.076 joules
Estimated Spark Energy: E = VAt = (2kV)(80ma)(0.8ms) = 0.120 joules12 Volts @ 5 amps held for 0.002 seconds delivers 0.12 joules.
1 joule = 1 watt-second
http://www.dtec.net.au/Ignition%20Coil%20Dwell%20Calibration.htmAn important operating parameter is "dwell time" or coil "on" time. This is the amount of time the primary current is given to ramp up to the coil operating point; This allows the iron core to build up to its maximum magnetic field strength. This interval is typically about 3 ms (or less) for an automotive application with a 12 volt supply. Lesser times result in lesser energy output, but longer times will not store more magnetic energy because of magnetic "saturation" of the core, and will simply result in excessive coil heating. The energy stored in an inductor is E = 1/2Li2 and so small changes in current rampup (or dwell time) result in large changes in energy.
Somewhat related to the ignition coil is the flyback transformer. Both have monopolar outputs but neither are true transformers. Transformers are designed to transfer energy through magnetic coupling, usually in a continuous, bipolar fashion. Inductors are designed to store energy in a magnetic medium and then release it in a monopolar pulse.
The purposes are also different. An ignition coil is intended to produce a spark, whereas a flyback is typically used to produce a "steady" high voltage DC potential in electronic devices like TV sets and switched-mode power supplies. They may have multiple secondary windings for various voltages, along with diodes and capacitors for filtering. They may also be used to produce "swept" or "ramped" DC voltages such as for horizontal scan in a TV. In that application the voltage change is gradual, rather than sudden, and linearity (enhanced by good magnetic design) is important. Some links:
"Flyback transformer" http://en.wikipedia.org/wiki/Flyback_transformer
"Flyback Inductor & Transformer Theory", http://www.butlerwinding.com/store.asp?pid=28336
"Inductor and Flyback Transformer Design", http://www.ti.com/lit/ml/slup127/slup127.pdf
"Designing Flyback Transformer for Discontinuous Mode", Keith Billings http://powerelectronics.com/site-files/powerelectronics.com/
files/archive/powerelectronics.com/mag/Keith%20Billings%20April%202003.pdfAlso, old battery-powered vacuum tube era radios often used special mechanical vibrating reed switches and real transformers to generate high voltages required by the vacuum tubes. See
"Vibrator Power Supplies", R. J. Rawlings, http://paleoelectronics.com/RDH4/CHAPTR32.PDF
"Understanding Ignition waveforms" http://www.motor.com/magazine/pdfs/052005_04.pdfCapacitor Discharge Ignition
http://en.wikipedia.org/wiki/Capacitor_discharge_ignition
http://en.wikipedia.org/wiki/Transformer_types#Pulse_transformer
http://en.wikipedia.org/wiki/Schmitt_trigger
http://www.worldphaco.net/uploads/CAPACITIVE_DISCHARGE_IGNITION_vs_MAGNETIC_DISCHARGE_IGNITION..pdfAnd there are such things as high voltage DC transformers that are not just oversized utility power transmission line transformers. One of these is the Insulated Core Transformer; see patents US3187208A.pdf US3274526A.pdf US4338657.pdf and http://cas.web.cern.ch/cas/pruhonice/pdf/dc-accel-DB1.pdf http://proceedings.aip.org/resource/2/apcpcs/1149/1/1099_1?isAuthorized=no http://www.freepatentsonline.com/EP0516454A1.pdf
See also the links at: http://scripturalphysics.org/4v4a/CapacitorTests/CapacitorTests.html
Now lets consider some characteristics about the various types of coil windings.
Modern induction coils generally use simple, multilayer helical windings. This is made possible by modern insulation coatings such as Formvar, Teflon, Nylon, Kynar, silicone, etc., which perform a lot better than the tar or shellac soaked double-cotton coverings of the old days. Wire is wound onto a cylindrical mandrel (a cardboard tube or nylon coil form) as it rotates. The winding starts out, say, at the left end, and proceeds to the right end, at which point it goes back, right-to-left this time, across and on top of the first layer of wire, with the mandrel still rotating in the same direction. The process is repeated until several layers are built up. This is the simplest, most intuitive way of winding an induction coil.
But it does have a disadvantage. One coiled layer of wire will induce a certain voltage, V, at the rightmost end relative to the starting point at the left (which would be the reference for zero volts). The second layer coming back to the left end will have a potential of 2V. With modern insulation this is usually not a problem. But with very high voltages another scheme might be used. Instead of winding the layers back-and-forth, they can be wound in one direction, say left-to-right only. At the rightmost end, the mandrel is stopped and a "carriage return" operation is done to bring the wire straight back to the left end. The operation then resumes with another layer wound left-to-right. This results in a maximum potential difference between layers at the winding ends of only V instead of 2V. This lowers the electrical stress on the insulation.
Still another winding technique can be used for even higher voltage operation: the pancake winding. Says Wikipedia:
"To prevent the high voltages generated in the coil from breaking down the thin insulation and arcing between the secondary wires, the secondary coil uses special construction so as to avoid having wires carrying large voltage differences lying next to each other. The secondary coil is wound in many thin flat pancake-shaped sections (called "pies"), connected in series. The primary coil is first wound on the iron core, and insulated from the secondary with a thick paper or rubber coating. Then each secondary subcoil is connected to the coil next to it, and slid onto the iron core, insulated from adjoining coils with varnished paper disks. The voltage developed in each subcoil isn't large enough to jump between the wires in the subcoil. Large voltages are only developed across many subcoils in series, which are too widely separated to arc over. To give the entire coil a final insulating coating, it was immersed in melted paraffin wax or rosin, and the air evacuated to ensure there are no air bubbles left inside, and the paraffin allowed to solidify, so the entire coil is encased in wax."
As such, pancake windings have less insulation stress, better cooling, and lower inter-winding "parasitic" capacitance. They are still just coils; there is nothing mysterious about them.
The intrawinding capacitance can be reduced even more by using a zigzag pancake winding technique (also known variously as "honey comb", "basket weave", and "spider wound") that was used in the old radio choke coils and Intermediate Frequency (IF) transformers. The layers cross at an angle instead of being parallel to each other. A special cam-operated coil winder is used to wind these kinds of coils. These coils, having less intrawinding capacitance, are more "purely inductive" (somewhat less stray capacitance) and have higher self-resonant frequencies, which is an important factor for radio sections operating at several megahertz. See http://www.youtube.com/watch?v=FIOocMoRsYQ http://www.paleoelectronics.com/RDH4/CHAPTR11.PDF http://www.paleoelectronics.com/RDH4/
Honeycomb coil winding operation
http://www.youtube.com/watch?v=TXP1-fdYKVUSpider wound coil (enlarged)
http://en.wikipedia.org/wiki/Inductor
An altogether different winding problem is encountered with high voltage pulse transformers. These are designed to handle 3 million volt pulses with enormous currents and fast rise times, which in turn require low inductance, low capacitance, and low resistance. But the transformer must be large to handle the high voltage. These will always be air core transformers typically constructed from sheet copper, with "graded" windings and no magnetic materials. They typically have less than a 1:7 turns ratio and are connected as an autotransformer to reduce DC flashover between what would otherwise be separate primary and secondary windings. Corona is controlled by tapering or "grading" the winding layers to reduce between-layer voltage gradients. Large fields will still develop at the edges of the copper but these can be controlled with semiconductive coatings (copper sulfate soaked blotting paper, zinc oxide, corona dope, etc) that help to even out the fields. (If you are having trouble visualizing what this thing looks like, make a big paper copy of the "Form of Copper Winding" shown in the diagram; roll it up, starting at its left end, around a soup can. This will help you understand the Cross Section diagram.)
J.C. Martin on Pulsed Power, J.C. Martin (1996) p. 37
The large size and spacing creates large leakage inductance. This can be controlled with two auxiliary windings:
"High-voltage pulse transformers are often used in association with high-voltage pulse generating circuits to further increase the pulse output voltage level. However, because of the transformer parasitic elements involved, the transformer is the critical device in shaping the rising characteristics of the output pulse. One of the techniques usually adopted to decrease the leakage inductance of the transformer adds two auxiliary windings to the transformer. If properly used, these auxiliary windings reduce the leakage flux and, therefore, the leakage inductance. As a result the pulse rise time is reduced." ("Rise time reduction in high-voltage pulse transformers using auxiliary windings", Redondo, L.M. (2002) IEEE Transactions on Power Electronics )
Inductance lumps (at tight bends, etc.) must be avoided, as these will generate high voltage spikes when hit with fast changing, high current pulses. Otherwise, the insulation requirements for fast pulses are not as stringent for those of slower pulses. With the former, disastrous leakages simply don't have time to develop. Still, a transformer like the one above will be immersed in oil.
You will also encounter "bifilar" ("two-filament") windings when exploring this topic. There are four categories (http://en.wikipedia.org/wiki/Bifilar_winding ; http://en.wikipedia.org/wiki/Bifilar_coil ):
1. parallel-wound, series connected
2. parallel-wound, parallel connected
3. counter-wound (series)
4. counter-wound (parallelThe second category is probably the most common. It is commonly used to make non-inductive wirewound resistors. The winding loops back on itself such that the direction of forward and returning currents are equal and opposite. The two magnetic fields thus cancel, and the arrangement has negligible inductance. A shorter version is called a "hairpin winding". (See also: http://en.wikipedia.org/wiki/Ayrton-Perry_winding )
These windings appear a lot in the "free energy" literature, where you will see references to "scalar waves", along with a lot of impressive, but obfuscatory technobabble. For less ambiguity, I call these "A with no B" windings because the magnetic B fields cancel out, but the vector potential A field still exists. The A field is apparently not just a mathematical artifact used to derive the B field, but has an actual physical existence with demonstrable effects. See Motion Couplers . This article also shows that all potential fields are based on temporal motions, which makes them "non-local" in a spatial reference system. The directional properties are due in part to the way they couple with the reference system; there is actually more to these fields than the reference system can depict. So the term "scalar" may indeed be appropriate in a limited sense. But "wave" is not. Potential fields have infinite propagation velocity; their effects are felt truly instantaneously, with no aberration or spatial propagation delay. There is nothing that "waves", at least in the sense of wave propagation, as in the case of radio or sound waves. With fields, oscillations at the generator will be detected instantly at the receiver, even if it is light years distant. See articles about the Speed of Gravity and the Speed of Electric Fields. Perhaps the term "longitudinal wave" is a misnomer being used to describe these characteristics.
A parallel wound, series connected bifilar winding is shown in Tesla's 0512340 patent. Fig.1 just shows an ordinary flat "pancake" winding (single wire). Fig. 2 shows the bifilar winding (two parallel wires, like zipcord or lamp cord, wound in one operation) along with the series connection:
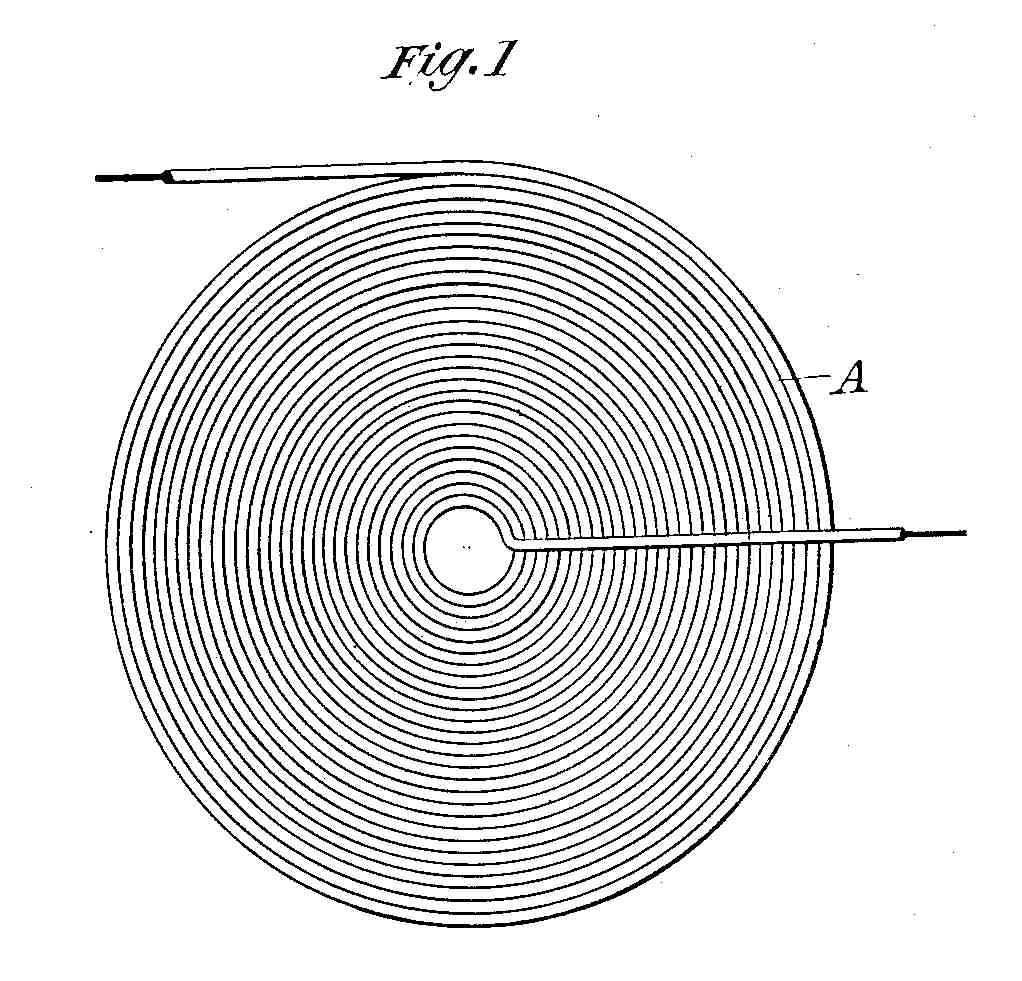
Fig1: ordinary spiral "pancake" winding (one wire) Fig2: bifilar series connected (currents in same direction)Tesla describes these different windings and their purpose in his patent:
Figure 1 is a diagram of a coil wound in the ordinary manner. Figure 2 is a diagram of a winding designed to secure the objects of my invention.
Let A, Figure 1, designate any given coil the spires or convolutions of which are wound upon and insulated from each other. Let it be assumed that the terminals of this coil show a potential difference of one hundred volts, and that there are one thousand convolutions; then considering any two contiguous points on adjacent convolutions let it be assumed that there will exist between them a potential difference of one-tenth of a volt. If now, as shown in Figure 2, a conductor B be wound parallel with the conductor A and insulated from it, and the end of A be connected with the starting point of B, the aggregate length of the two conductors being such that the assumed number of convolutions or turns is the same, viz., one thousand, then the potential difference between any two points in A and B will be fifty volts, and as the capacity effect is proportionate to the square of this difference, the energy stored in the coil as a whole will now be two hundred and fifty thousand as great. Following out this principle, I may wind any given coil either in whole or in part, not only in the specific manner herein illustrated, but in a great variety of ways, well-known in the art, so as to secure between adjacent convolutions such potential difference as will give the proper capacity to neutralize the self-induction for any given current that may be employed. Capacity secured in this particular way possesses an additional advantage in that it is evenly distributed, a consideration of the greatest importance in many cases, and the results, both as to efficiency and economy, are the more readily and easily obtained as the size of the coils, the potential difference, or frequency of the currents are increased.
Tesla's terminology is a bit confusing here. The words "capacity effect" actually mean "energy", not "capacitance". The energy stored in a capacitor is E = 1/2 CV2 which means if you double the voltage across the capacitor, the electrical energy stored is quadrupled. Tesla's coil in Fig. 2 uses a series connection of two insulated wires to impose 50 volts across the stray capacitance per turn instead of only the 0.1 volt that would be the case with a single wire. This gives an energy increase of 250 per turn, and thus gives 250,000 for 1000 turns. The advantage of this arrangement, according to Tesla, is even distribution of energy in the stray capacitance, "a consideration of the greatest importance in many cases", as well as easier construction of large, high frequency coils (likely without those messy, separate capacitors or a "top load" toroid).
Note that Tesla's arrangement makes use of existing stray capacitance. It is possible to deliberately add stray capacitance by impregnating the winding with an interlayer dielectric. Back then it would probably have been mica powder and beeswax. Today it would be something like epoxy with barium titanate powder. Both the insulation and the potting compounds can be chosen to give the desired resonant frequency and energy capacity (if you know what you are doing). Usually, though, more capacitance is not wanted. More will be said about this in Part 2.
Helmholtz coils are another coil configuration you might see sometimes. They will not be used here, but you should know something about them. They are often used to cancel the effects of the Earth's magnetic field as when weighing various configurations of magnets, or detecting effect of current loops . See:
http://en.wikipedia.org/wiki/Helmholtz_coil
http://en.wikipedia.org/wiki/Maxwell_coil
http://en.wikipedia.org/wiki/Teltron_TubeSee also:
http://en.wikipedia.org/wiki/Capacitance
http://en.wikipedia.org/wiki/LC_circuit
http://en.wikipedia.org/wiki/Inductor
https://en.wikipedia.org/wiki/Magnetic_core
http://www.pa2mrx.nl/UK/coil%20homebrewing_uk.htm
http://www.oldradioworld.de/gollum/honey.htm
Replication schemes for Farrow and Piggott experiments
The configuration for the attempted replication of the Piggott experiment is shown in the following diagram:
Piggott does not describe his setup in detail. Hence, some assumptions are necessary and various different configurations will have to be tried. What seems fairly certain from the1911 sketch is that he was using an industrial strength electrostatic machine, and the experiment involved pulsed power, and that the layout was similar to that shown above. A wire conductor is used to charge up the ball electrode, and presumably, a spark gap is used to discharge the ball when the voltage became high enough. This would result in a waveform with a slow rising edge and a fast falling edge. Because he was testing his machine for wireless telegraphy, the discharges were probably repeated several times per second.
It is not clear however, where the spark gap and leyden jar were in the circuit, or if there even was a leyden jar in the circuit (a leyden jar would affect the symmetry of the rise and fall times as seen from the metal ball electrode). The spark gap was probably the ball type that was commonly used around 1911. Nowadays, a biconical impedance controlled gap or a pseudospark gap could be used for faster switching resulting in improved waveforms.
The electrostatic machine proposed for this attempt at replication is a van de Graaff generator similar to the type invented by American physicist Robert J. Van de Graaff in 1929. It is a robust version that uses a 14" top electrode (+) with a double roller and sprayed charge arrangement that is considerably more powerful than those used in school classrooms. It can be built with parts that are readily obtainable or easily made. The maximum voltage is nominally 500,000 volts (with the top electrode covered with a plastic bag). The short circuit current output is unknown but is hoped to be at least 100 microamps.
The questions this experiment is intended to answer are:
1. Are any weight loss or levitation effects discernable in this experiment? Do these effects require several seconds or minutes to become manifest? (the expected delay has to do with atomic spin systems; See Rotations of Rotations )
2. Can small metallic (silver) spheres (or balls) be "floated" between the HV sphere and ground plate? If so, are there any discernable "dark band" effects?
3. Do objects exposed to the field momentarily retain a weightloss for a few seconds when removed from the field?
4. Do the decay rates of radioactive materials change when exposed to the field?
5. How do the above effects depend on the configuration of the spark gap, leyden jar, terminal polarity, etc.? Do external high frequency, high voltage AC fields produce any noticeable changes?
_____
For the Farrow experiment, the configuration is as shown below:
The configuration for the Farrow experiment is even less clear than that for the Piggott experiment. Presumably he was using a Ruhmkorff coil which would have produced monopolar, pulsed high voltage. This has been approximated by using an ignition coil and a robust Pulse Width Modulator intended for use with such coils. The specific parts proposed are:
Power Pulse Modulator, A Versatile Square Pulse Generator, Model: PWM-OCXIa, Type: High Voltage, 9A, 500V, 1.5 MHz
http://www.rmcybernetics.com/shop/cyber-circuits/pulse-generators/pulse-modulator-ocxi (description)
http://www.rmcybernetics.com/files/pdf/PWM-OCXiv2.pdf (manual)ACCEL Super Stock Universal Performance Coil, 12 volt, #8140, oil filled (primary 1.5 ohms, secondary 9.67 kiloohms; inductance is not given but 4 to10 milliheneries is typical of this type; purchased at a local autosupply store.
The coil can be protected by a voltage limiting spark gap set to fire at 20,000 volts. The PWM controls can be set slightly below the firing point, as no sparks are desired in this experiment. The repetition rate should be about 20 to 200 pulses per second.
See also:
http://www.dnatube.com/video/6627/Pulse-width-modulation-PWM-Tutorial
http://www.rmcybernetics.com/projects/DIY_Devices/homemade_ignition_coil_driver.htmAn ignition coil produces a pulse with a rise time probably in the neighborhood of 50 microseconds. For these experiments, that is a long time. The limitation comes from the "sudden" collapse of the magnetic field, which is sudden enough for an automotive ignition system, but probably barely adequate for these experiments. A pulse from a Ruhmkorff coil would have similar characteristics, except with much higher voltage. Faster rise times can be produced with peaking techniques referenced in Capacitor Tests .
Either kind of coil would supply much more current than is possible to get from a laboratory strength van de Graaff.
Note that the presumably critical element in the Piggott experiment is a fast fall time and that in the Farrow experiment is a fast rise time. Both are setup to produce positive (+) monopolar pulses. Unfortunately, many details are not clear and so a lot of different configurations must be tested. Additionally, this kind of science is still weird and largely counter-intuitive at this time; do not be afraid to try things that are "pointless, and obviously won't work".
The questions this experiment is intended to answer are:
1. Can an apparent weight loss be detected after running a selected configuration for a minute or two?
2. Can small metallic spheres (or balls) be "floated" Piggott-like between the HV sphere and ground plate? Are there any discernable "dark band" effects?
3. Do objects exposed to the field momentarily retain a weightloss for a few seconds when removed from the field?
4. Do the decay rates of radioactive materials change when exposed to the field?
5. How do the above effects depend on the system configuration (layout of the wire, pulse repetition rate, etc)?
_____
These are "proof of principle" experiments only. They are designed to detect an effect, not accomplish anything practical.
Warning: These advanced versions are not "do it at home alone" projects. These are very dangerous machines.
Rotating pulsed electrical fields
Piggott charged and then discharged one sphere repeatedly several times a second. But a little thought shows he could just as well have spread out these charge/discharge cycles spatially. For example, instead of several electrical pulses per second on one single sphere, he could have done one electrical pulse on several different spheres per second, the spheres being arranged in a circle. A single rotating electrode, much like that in a car's ignition distributor, would spark charge one electrode in the circle at a time. The charge would then dissipate to ground through a high voltage resistor. Hence, the same amount of power with the same number of discharge/charge cycles is distributed around a circle, resulting in a rotating field of pulsed electrical discharges with asymmetric time derivatives (they would, however, be the reverse of what Piggot probably used).
Large spatially rotating and fast time-changing electric fields have important magnetic effects which may be relevant to the application of antigravity.
<the rest of this section cannot be published at this time>
—